Un bosque con 100 polígonos

**3dpoder** · 07-01-2007, 01:02

Introducción. Desde los primeros tiempos de la animación 3d se han utilizado muchos trucos para representar árboles en nuestras escenas. Uno de los más conocidos -utilizado ampliamente en los entornos de los videojuegos- Es el de los billboard tres consistente en colocar la imagen frontal de cada árbol sobre un plano que siempre apunta hacia la cámara. De ese modo podemos poblar una amplia superficie con decenas o cientos de planos -árboles- Que siempre nos miran de frente. Una variante ligeramente mejorada consiste en realizar un render frontal y otro lateral y colocarlos sobre dos planos ortogonales -un aspa- O incluso sobre 3 planos a 60º de desfase. En estos últimos casos no haremos que los planos nos miren sino que al ir girando en torno a ellos nos irán mostrando los sucesivos 2 o 3 puntos de vista previamente calculados del árbol.

De esta manera conseguiríamos no tener que lidiar con muchos miles o millones de polígonos, ya que un árbol puede llegar a tener una geometría muy densa -si queremos representarlo de un modo detallado y realista- Por lo que cuando necesitamos poblar una escena con una gran cantidad de ellos se sobrecarga de tal manera que se hace inmanejable. El problema de los billboards es que, con cierto tipo de movimientos y niveles de acercamiento, el truco se hace muy evidente, arruinando todo nuestro trabajo.

Existen soluciones intermedias consistentes en crear versiones de árboles con una cantidad reducida de polígonos: si un árbol muy detallado fácilmente puede pasar de los 100.000 polígonos, podemos crear versiones más ligeras con sólo 1.000 o 2.000 polígonos. Pero pese a ello, si necesitamos trabajar con cientos o miles de árboles, nos siguen generando geometrías bastante pesadas. Con el problema añadido de que no podemos acercarnos mucho, ya que enseguida se hace palpable su falta de resolución.

Vamos a ver una técnica que lleva un paso más, allá la de los billboards, permitiendo acercarnos bastante a cada uno de nuestros árboles durante una animación y girar en torno a ellos usando tan sólo un polígono (bueno, para ser exactos: dos polígonos por árbol). Podríamos definirla como una versión casera de la tecnología empleada por los modelos RPC de la compañía Archivision.

Preparando el material.

Para empezar creamos un árbol 3d muy detallado, sin importarnos demasiado el número de polígonos que lo formen. Lo que debemos buscar es que resulte lo más realista posible, incluso en las distancias cortas, cuando su presencia llene toda la pantalla de nuestra animación.

Existen varias compañías que venden buenos modelos ya creados o que comercializan herramientas para diseñar nuestros propios árboles. En cualquier caso, modelar y texturizar un árbol para que resulte realista y convincente tiene sus técnicas, en las que aquí no vamos a profundizar demasiado.

Tan sólo comentar que es conveniente crear varios grupos de hojas diferentes, tratarlas como superficies planas o ligeramente curvadas -pero de contornos rectangulares- Y conseguir su acabado superficial y el recorte exacto mediante la utilización de texturas y clipmaps (mapas de recorte) aplicados por coordenadas UVS. El tronco y las ramas también conviene que tengan asociados un mapeado UV para poder texturizarlos cómodamente con la ayuda de una buena textura de corteza tileable (repetitiva, azulejable).

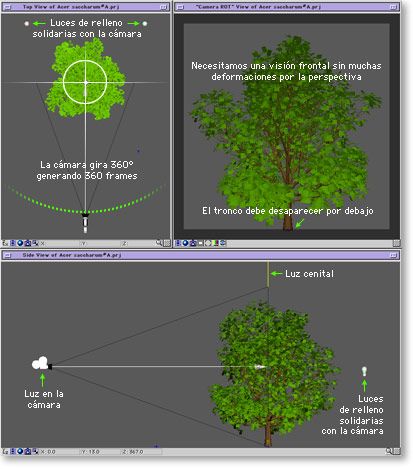
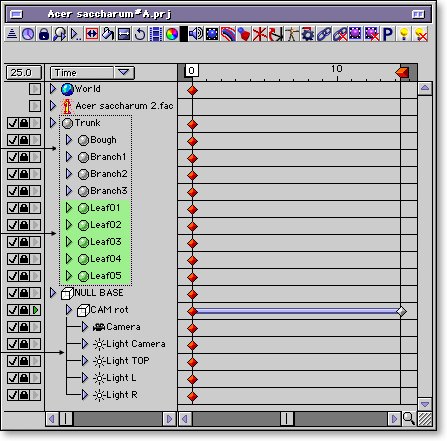
Lo más importante: colocamos una cámara enfrente de nuestro árbol y hacemos que gire 360 grados alrededor de el durante 360 fotogramas (*). Así tendremos 1 fotograma por cada grado de giro.

En los gráficos siguientes vemos la configuración:

para realizar el presente tutorial he partido de un modelo de árbol con 175.000 polígonos y lo he texturizado de un modo muy básico y sencillo -sin invertir demasiado tiempo, dicho sea de paso. He acabado generando una película de 1024 por 1024 píxels con 360 fotogramas y sus correspondientes canales alfa (que servirán para recortar las siluetas, tanto de los propios árboles como de los planos que proyectaran la sombra). Esto nos permitirá acercarnos mucho a nuestro árbol, ya que una imagen PAL tiene 720 o 768 píxeles de anchura, así que, nuestro modelo podría llenar toda la pantalla, de sobra. Si no necesitamos acercarnos tanto -como generalmente suele ocurrir- Podemos generar una movie más reducida, de 512 o incluso de sólo 256 píxeles de lado.
(*) nota: cuidado al generar la movie de 360 grados con el ángulo de giro que hayáis seguido. No es lo mismo seguir una orientación horaria que anti-horaria. En mi caso yo he trabajado en el sentido de las agujas del reloj [ gracias por el apunte, Alberto ].
lo que vamos a hacer, en resumen.

Muy bien ¿y que hacemos ahora con nuestra película de 360 frames filmada alrededor de nuestro árbol? Pues dicho en pocas palabras:

vamos a texturizar con ella un plano, le vamos a decir que siempre apunte hacia la cámara y que nos muestre en cada momento el fotograma correspondiente al ángulo con el que lo estamos mirando.

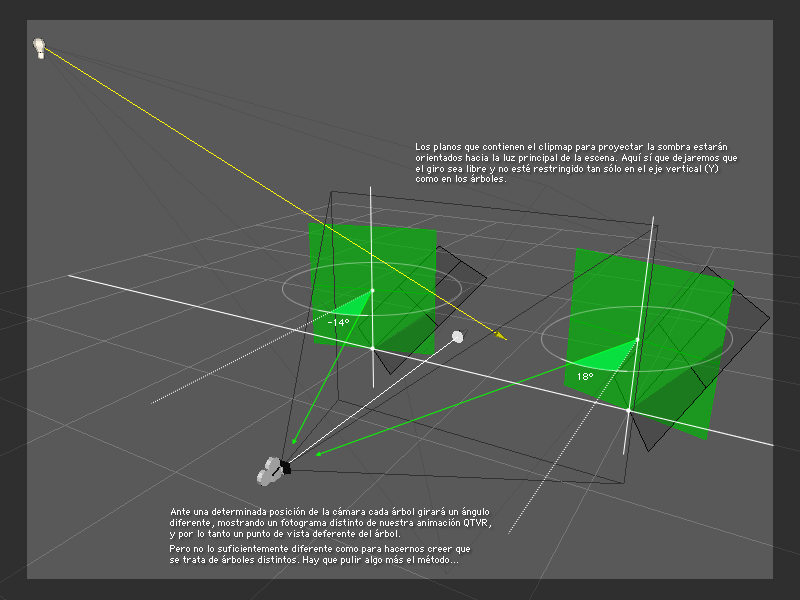
eso es todo, así de simple. Pero vamos a verlo todo con más detalle. En el siguiente gráfico vemos la configuración básica: colocamos un plano donde necesitamos cada árbol y los texturizamos con nuestra movie. Tan sólo necesitamos saber el ángulo con el que miran hacia la cámara para que en cada caso nos muestren el fotograma correspondiente a esa posición (enseguida veremos cómo hacerlo).

Por otro lado, necesitamos crear un segundo plano por cada árbol -linkado a éste- Que contendrá una imagen fija, o mejor dicho: una de las 360 imágenes alfa que también habremos generado previamente al renderizar nuestra movie virtual. Esa imagen alfa -un fotograma cualquiera, aleatorio, pero constante- Recortara ese segundo plano y proyectara la sombra correspondiente a nuestro árbol. Y a este plano le ordenaremos que siempre apunte hacia la fuente de luz principal, la que proyecte sombras. Lógicamente a nuestro programa tendremos que indicarle que de estos últimos planos recortados con el clipmap sólo se renderice su sombra proyectada, y por contra, a cada plano que contiente la imagen -también recortada con su clipmap correspondiente- Del árbol le indicaremos que no proyecte sombra alguna.

En pocas palabras, por cada árbol tendremos:
- Un plano que siempre apunta a la cámara, texturizado con la animación recortada de nuestro árbol y que no proyecta sombras.
- Otro plano que siempre apunta a la fuente de luz, recortado por un clipmap fijo y del que sólo se renderiza su sombra proyectada.

De este modo, conforme giremos entorno a un árbol, el plano que lo contiene siempre nos estará mirando y nos mostrara el fotograma correspondiente al punto de vista desde el que lo observamos. De este modo conseguiremos engañar a nuestro ojo haciéndole creer que estamos girando en torno a un objeto tridimensional, cuando tan sólo estamos viendo una sucesión de imágenes. Fácil ¿no?

La clave del proceso: el script.

Bien, en todo este proceso que -creo- Resulta muy sencillo de entender, sólo hay un pequeño detalle que tendremos que solventar:

¿cómo lograr que nuestro plano-árbol nos muestre en cada momento el fotograma de la película correspondiente al ángulo con el que lo estamos mirando?

la respuesta es corta: mediante un sencillo script, una orden de programación.

Prácticamente todos los programas 3d incorporan la posibilidad de utilizar scripts: mel en Maya, cofe en Cinema, maxscripts, etc. Posiblemente muchos de los que leáis este tutorial nunca habéis creado ni utilizado un script. Yo jamás he estudiado ningún lenguaje de programación, pero con un poco de voluntad resulta accesible hacerse con los principios más básicos que nos permitan crear algún script sencillo. Algo que puede sernos de una enorme ayuda e evitarnos muchísimo trabajo pesado cuando trabajamos en 3d, especialmente si estamos creando una animación con tareas repetitivas o que implican lidiar con multitud de objetos.

Para el script de este tutorial he utilizado xpressionist, el lenguaje interno de electricimage. Explicaré paso a paso las pocas líneas del código para que cada cual pueda interpretarlo y trasladarlo a su correspondiente software. Lo importante es que en cada paso se entienda el concepto, porque está clarísimo que luego podréis hacerlo siguiendo otros caminos (cada programa es diferente y plantea unas paticularidades propias. Y al fin y al cabo, siempre hay muchas formas de llegar al mismo sitio).

Este sería un script básico (e ideal, el definitivo habrá que pulirlo un poco, dependiendo del comportamiento de vuestro programa) que haría lo que más arriba hemos visto:
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800> <tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td>arbol1. Yaw_y=look at(arbol1. Position,cámara. Position). Y;
Arbol1. Diffuse_arbol360movie. Frame = round(arbol1. Yaw_y),
Arbol1. Clip_arbol360movie. Frame = round(arbol1. Yaw_y),</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>.

Veamos lo que controla cada una de estas líneas.
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800> <tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>arbol1. Yaw_y=look at(árbol. Position,cámara. Position). Y; </td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>
Con esta línea estamos ordenando a nuestro árbol arbol1 que mire a la cámara. El giro en el eje y yaw_y del plano que lo contiene estará controlado por la posición relativa de cada elemento -arbol. Position y cámara. Position-, usando la función look at y restringiendo ese giro exclusivamente al eje Y.
nota aclaratoria: supongo que la mayor parte de programas 3d ya llevan incorporado un sistema de constraints que permite que una orden tan sencilla como un lok-at sea controlada de un modo directo, sin tener que recurrir a scripts como éste. Electricimage, de hecho, también tiene unos potentes constraints que permite gestionar el lok-at en tiempo real -entre otras cosas. Pero me he visto obligado a no utilizarlas y controlar ese parámetro a través de un script, porque de lo contrario los valores angulares que tomaba el plano dirigido por los constraints no eran tenidos en cuenta por el resto del script. No sé si se puede considerar a esto como un bug -fallo- O una limitación generalizada. En cualquier caso, lo aclaro aquí para que, si os sucede algo similar con vuestro software favorito, tengáis en cuenta la posibilidad de controlar el lok-at opcionalmente mediante scripts.
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800> <tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>arbol1. Diffuse_arbol360movie. Frame = round(arbol1. Yaw_y),</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>
Una vez que determinamos el ángulo de giro del eje y en nuestro árbol arbol1. Yaw_y calculamos su valor entero y redondeado round para indicarle a nuestra textura animada arbol360movie el número del fotograma frame que debe mostrar en el canal de color Diffuse. Esto es muy importante, ya que nuestro plano puede tener un ángulo de giro con varios decimales (17,1679º) pero lamentablemente no contamos con un frame 17,1679 en nuestra textura animada. Por ello deberemos quedarnos con el valor más aproximado y usar el frame 17.
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800> <tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>arbol1. Clip_arbol360movie. Frame = round(arbol1. Yaw_y),</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>
Esto es básicamente lo mismo: igual que con el canal de color hacemos con el mapa de recorte de nuestro árbol clip.

pero las cosas suelen no ser tan simples.

Hasta aquí es todo muy bonito y sencillo. Pero nos encontramos con un problema bastante lógico en cuanto empezamos a poblar nuestra escena con muchos árboles: se hace evidente que todos ellos son el mismo árbol, porque, aunque cada uno de los planos que los soporta tiene un valor de giro específico -como resultado de estar mirando a la cámara-, la realidad es que, si nos alejamos un poco, el aspecto en los árboles cercanos es muy similar.

Para poder entender y solucionar mejor este problema podemos sustituir la textura animada de un árbol por otra textura mucho más gráfica. Una especie de checkgrid animado: generamos una movie de 360 frames haciendo que vaya cambiando de color y recorriendo todo el espectro (esto es muy sencillo de obtener con After Effects, por ejemplo). Y de paso aprovechamos para incluir en cada frame un número correspondiente al valor numérico de ese frame.

Cuando aplicamos esa textura de chequeo a nuestro conjunto de planos y renderizamos un recorrido enseguida aparece el problema del que hablamos. En la siguiente animación podemos verlo de un modo muy gráfico:

table border=0 cellpadding=0 cellspacing=0 width=800><tbody><tr valign=top><td width=290>en la izquierda vemos como en todos los planos aparecen unos colores distintos, pero muy similares, ya que, aunque su ángulo de giro es diferente, se aproxima mucho. Si sustituyéramos la textura de colores secuenciales por la de nuestro árbol virtual todo el tiempo estaríamos percibiendo un punto de vista muy similar del árbol. Nos daríamos cuenta de que es el mismo objeto, arruinando nuestra animación.
/td> <td> </td> <td width=200>en el centro tenemos la textura animada que hemos generado en After Effects mostrando todos los colores del espectro, al mismo tiempo que en cada fotograma aparece impreso su número de orden. Luego explicamos el número más pequeño que aparece debajo. ;-)
/td> <td> </td> <td class=petita width=290>en la parte derecha vemos cómo hemos logrado obtener unos colores muy distintos en cada plano. Hemos introducido un punto de partida aleatorio en la textura de colores, de tal modo que, aunque evoluciona correctamente dentro de cada plano, cada uno de ellos tiene un aspecto diferente. Al sustituir los colores por nuestro árbol en cada plano aparecerá un punto de vista muy distinto. </td> </tr> </tbody></table> <table border=0 cellpadding=0 cellspacing=0 height=30 width=800> <tbody><tr> <td>(importante: es necesario tener instalado QuickTime para poder ver la animación)
/td> </tr> </tbody></table> <table border=0 cellpadding=0 cellspacing=0 height=20 width=800> <tbody><tr> <td>
/td> </tr> </tbody></table> la conclusión que extraemos de la animación de prueba que hemos obtenido es que necesitamos hacer que cada árbol muestre un frame correspondiente al ángulo con el que mira a la cámara pero con un desfase aleatorio añadido, para que todos los árboles parezcan distintos. Pero cuidado: el desfase debe ser aleatorio, pero sólo en el punto de arranque, no puede ir cambiando aleatoriamente para cada frame (porque en ese caso tendríamos una auténtica locura de animación) sino que deberá ir avanzando o retrocediendo controlado por el valor del ángulo que tenemos en cada instante.

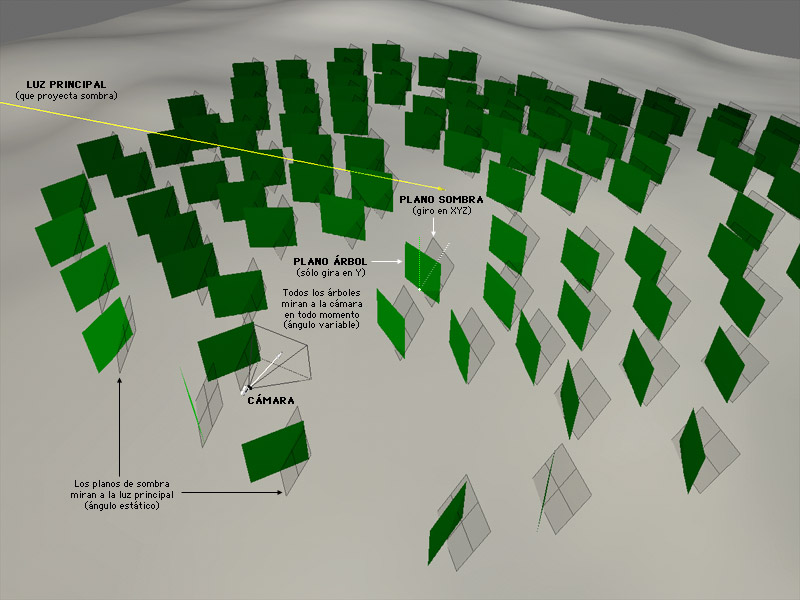
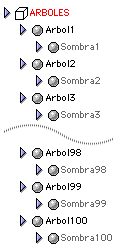
Y por otro lado, necesitamos crear un script potente y flexible que nos permita gestionar un número elevado de árboles sin tener que ir indicando árbol por árbol lo que tiene que hacer cada uno. Imaginemos que queremos controlar un pequeño bosque de 100 árboles. Éste será el aspecto que tendrá:

puliendo el script.

Veamos una solución que permitirá controlar el comportamiento de todo ese conjunto (una de las muchas posibles, porque seguro que habría otras formas de conseguirlo).
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800> <tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>for (i=1, i<=100, i=i+1)
{
$árbol = árbol+i;
$sombra = sombra+i.
$árbol. Yaw_y = look at($árbol. Position,cámara. Position). Y.

If ($árbol. Yaw_y >= 0)
A = $árbol. Yaw_y;
Else.

A = $árbol. Yaw_y+360.

B=round(a)+pow(i,4).
$árbol. Diffuse_arbol360movie. Frame = b-((trunc(b/360))*360),
$árbol. Clip_arbol360movie. Frame = b-((trunc(b/360))*360).

C=pow(i,4).
$sombra. Clip_arbol360movie. Frame = c-((trunc(c/360))*360),
} </td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>.

E igual que antes, vamos a ver qué es lo que controlamos en cada apartado:
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800><tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>for (i=1, i<=100, i=i+1)
{
$árbol = árbol+i;
$sombra = sombra+i;</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td></tr></tbody></table>.

En nuestra escena tenemos 100 planos que contienen la misma animación de 360 frames de nuestro árbol y otros tantos planos utilizados para gestionar la sombra que debe trabajo cada uno de ellos. En nuestro proyecto, a cada uno de esos elementos, lo hemos renombrado como arbol1, arbol2, arbol3, sucesivamente hasta llegar a arbol98, arbol99 y arbol100. Con los planos que contienen el recorte de la sombra hemos hecho lo mismo: desde sombra1 hasta sombra100.

Para evitar tener que escribir un script larguísimo y repetitivo que le fuera ordenando a cada árbol lo que tiene que hacer, hemos usado una expresión del tipo for next loops -que tiene la propiedad de ejecutar una orden repetidamente sobre una sucesión de objetos hasta que la condición inicial definida es alcanzada- Combinándola con el uso de una variable string -que actúa como contenedor de una palabra.

Para entenderlo mejor: cada uno de nuestros árboles se llama arbol1, arbol2 etc, o sea, podemos escribirlo como una sucesión de objetos de la forma arbol+i, donde i es un valor que va variando desde 1 hasta 100 e incrementándose en una unidad cada vez (i=1, i<=100, i=i+1) y a la entidad resultante se la denominara con el término $árbol. Del mismo modo ocurre con los planos que contienen el clipmap que proyectara la sombra ($sombra = sombra+i). Así, si queremos aumentar el número de árboles de 100 a 200 sólo tendremos que rescribir un 200 donde ahora tenemos el 100.
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800><tbody><tr><td><table border=0 cellpadding=0 cellspacing=0 width=770><tbody><tr><td class=scripts>$árbol. Yaw_y = look at($árbol. Position,cámara. Position). Y;</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>
Ahora el giro en el eje y de cada uno de los árboles, desde el primero al último, está representado bajo la forma $árbol. Yaw_y y, de la misma manera que hemos explicado más arriba, viene controlado por su situación relativa respecto a la cámara en todo momento, mediante el uso de la función look at.
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800><tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>if ($árbol. Yaw_y >= 0)
A = $árbol. Yaw_y;
Else.

A = $árbol. Yaw_y+360;</td></tr></tbody></table>
/td></tr></tbody></table>.

En una situación ideal bastaría con decirle a nuestro programa que para cada valor de un ángulo de giro de nuestro plano le asignara un frame determinado de la animación con nuestro árbol virtual: ¿22 grados de giro? Frame 22; ¿157 grados? Frame 157, etc.

Pero puede surgir un problema, dependiendo de cómo entienda la disposición de los valores angulares nuestro software 3d (o el sistema de scripting utilizado). ¿en qué punto está el ángulo 0º? ¿y el 90 grados? ¿y el 327º? ¿y si internamente nuestro programa en vez de entregarnos un ángulo +270º nos da -90 grados?
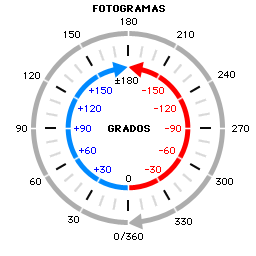
Resulta que +270º y -90 grados son el mismo ángulo exactamente, pero nosotros no podemos asignar un valor de frame igual a -90. Eso es exactamente lo que a mí me ha pasado al trabajar en este tutorial con mi software. O mejor dicho: no con el programa -electricimage- Sino con el sistema de scripting y la orden de generación del look at: me entrega unos valores angulares que van desde 0º a +180 grados pasando por +90 grados y desde 0º a -180 grados pasando por -90 grados (**).

La forma de solventar este problema es sumar a los valores angulares negativos la cantidad de 360, o sea, para el ángulo -120º usaremos el frame 240 (240º es igual a -120º + 360 grados). Eso es lo que gestionamos con estas cuatro líneas de código. Y al valor resultante, siempre positivo y con un valor entre 0 y 360, le llamaremos a.
(**) nota: por este problema he incluido los números más pequeños del checkgrid animado: contienen los valores negativos correspondientes a la zona en rojo del gráfico.

<table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800><tbody><tr><td><table border=0 cellpadding=0 cellspacing=0 width=770><tbody><tr><td class=scripts>b=round(a)+pow(i,4),</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>
Como ya hemos explicado antes, necesitamos convertir el valor del ángulo resultante a en una cantidad entera, sin decimales. Esto lo conseguimos mediante la orden round(a).

Y aquí viene una parte muy importante -que estoy seguro se podría haber resuelto de otras maneras-: necesitamos que cada árbol tenga un aspecto diferente que el que está a su lado, por eso queremos introducir un desfase en la secuencia de los frames que nos muestra cada uno. Mi primera idea fue utilizar un sumatorio añadiendo un valor aleatorio (un random) a cada árbol. El problema que surgía es que para cada frame de la animación resultante la expresión iba variando según ese valor aleatorio, de modo que todos los árboles iban generando un bailoteo en los frames que mostraban que desbarataba todo el proceso.

Tengo que volver a aclarar que no tengo ni idea de programación ni tengo la base técnica necesaria para lidiar con estas situaciones, pero estoy seguro de que se tiene que poder resolver el problema usando número aleatorios. Pero no supe resolverlo de ese modo ni quise dedicarle más tiempo.

Se me ocurrió, en cambio, una solución seguramente poco ortodoxa, pero que proporciona un resultado perfecto: al valor del ángulo que tiene un árbol i en un momento concreto le sumamos un número que siempre va a ser constante para ese árbol a lo largo de la animación, pero diferente al resto de los árboles. ¿Qué número? : una potencia del valor i, concretamente i elevado a 4 (pow(i,4)). Podríamos haber usado otra potencia cualquiera: 2, 3, 7, 29, no importa. La cuestión es que para cada árbol obtenemos un número único b que es igual a su valor angular entero sumado a un número constante a lo largo del tiempo, pero único: b=round(a)+pow(i,4).
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800> <tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>$árbol. Diffuse_arbol360movie. Frame = b-((trunc(b/360))*360),
$árbol. Clip_arbol360movie. Frame = b-((trunc(b/360))*360),</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>
El problema es que el resultado de la anterior fórmula b=round(a)+pow(i,4) nos va a dar valores muy altos, que se van a salir fuera del rango 000º - 360 grados. Para solucionarlo recurrimos a las matemáticas más elementales: el ángulo 367º es exactamente el mismo que 7º (367º = 360 grados + 7º), 723º es lo mismo que 3º (723º = 360 grados + 360 grados + 3º), 6169º es igual a 49º (6169º = 360 grados*17º + 49º).

Cualquier número que representa a un valor angular superior a 360 grados puede reducirse a su equivalente dentro de la circunferencia mediante un sencillo cálculo:
- Dividimos el número b para 360
- Nos quedamos con su valor entero trunc.
- El valor obtenido lo multiplicamos por 360
- Y el resultado se lo restamos a nuestro número inicial.

Esa es la formula que tenemos aquí: b-((trunc(b/360))*360).

Con el ejemplo 6169: 6169-((trunc(6169/360))*360) = 6169-((trunc(17,13611111111))*360 = 6169-(17*360) = 49.

Y ya sólo nos queda asignar a cada frame el valor obtenido de la anterior fórmula, tanto en el color ($árbol. Diffuse_arbol360movie. Frame) como en el mapa de recorte ($árbol. Clip_arbol360movie. Frame).
table background=deg_scripts, gif border=0 cellpadding=0 cellspacing=0 width=800> <tbody><tr> <td height=15>
/td> </tr> <tr> <td> <table border=0 cellpadding=0 cellspacing=0 width=770> <tbody><tr> <td class=scripts>c=pow(i,4).
$sombra. Clip_arbol360movie. Frame = c-((trunc(c/360))*360),</td> </tr> </tbody></table>
/td> </tr> <tr> <td height=15>
/td> </tr> </tbody></table>
No debemos olvidarnos de los planos que contienen el mapa de recorte que producirá la sombra proyectada por los árboles. Se supone que cada árbol debe ser (o por lo menos parecer) distinto, por lo tanto sus sombras deberían ser distintas también. Así que necesitamos aplicar un fotograma-alfa de nuestra textura animada en cada plano-sombra, diferente del que se aplique en los árboles de alrededor. A diferencia de los propios árboles, la sombra arrojada no debe cambiar en función del ángulo con que la miremos, es siempre la misma.

Así pues definimos un nuevo valor c que es igual a cuarta la potencia del valor i (c=pow(i,4)) de este modo nos aseguramos que cada árbol tiene un valor único diferenciado del resto y constante a lo largo de toda la animación. Fijémonos que no ira cambiando porque no le sumamos el ángulo que toma ni el árbol ni el plano de sombra, eso es indiferente. Lo que sí necesitamos es acotar el valor resultante dentro del rango 000º - 360 grados, para que siempre pueda aplicarse uno de los 360 fotogramas de nuestra textura animada. Para ello volvemos a aplicar la misma fórmula que antes: c-((trunc(c/360))*360).

Y el resultado es lo que se aplicará al mapa de recorte del plano-sombra: $sombra. Clip_arbol360movie. Frame.
conclusiones.

Todo esto es sólo el principio, esta técnica se podría mejorar mucho, atacando con diferentes detalles:
- Podríamos generar unos mapas de normales animados con nuestro árbol inicial 3d para añadir mucha más profundidad.

Deberíamos trabajar con más de un único árbol: quizá con 3 modelos de la misma especie, generando 3 películas de 360 frames que se irían distribuyendo aleatoriamente por todos los planos, para introducir mucha más variedad.

Podríamos generar diferentes resoluciones de una misma película VR (alta, a 1024px, media, a 512px, y baja, a 256px) para luego modificar el script de modo que asignara una u otra resolución dinámicamente, en función de la distancia de cada plano-árbol a la cámara.

Y a continuación podemos apreciar el resultado que proporciona al movernos por entre los árboles (cosa que no podríamos hacer utilizando simples billboards). Tened en cuenta que no se trata de un proyecto cuidado: he ido muy deprisa para montar toda la escena, no he cuidado especialmente el texturizado del árbol original (algo que resulta básico para obtener un buen resultado), todos los planos tienen exactamente el mismo tamaño (algo que deberíamos ir modificando, para introducir más variedad). Por favor: consideradlo únicamente como un test para probar la técnica.

Además, de la imagen fija podéis ver una animación de 4,5 Mb.

(Importante: es necesario tener instalado QuickTime para poder ver la animación).

No quiero despedir este tutorial sin mencionar algunas de la limitaciones de esta técnica (que las tiene).

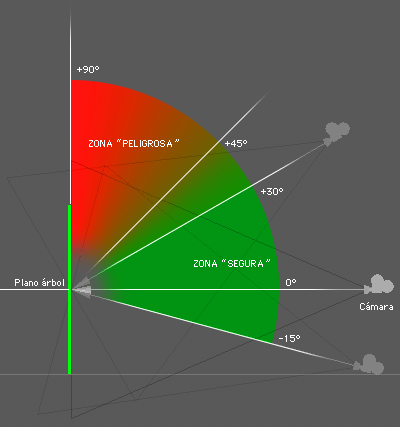
Al igual que con los billboards tradicionales debemos colocar nuestro ángulo de visión dentro de unos márgenes de seguridad. Una visión cenital, por ejemplo, se hace imposible. A la derecha vemos unos valores orientativos dentro de los cuales podemos movernos.

Debemos tener cuidado con la velocidad angular con la que nos movemos respecto a cada elemento: pensemos que hemos captado 360 fotogramas alrededor de un árbol, uno cada grado. Eso significa que hemos recorrido 360 grados en 14,4 segundos (360/25). Si necesitamos movermos muy despacio alrededor de un árbol, o queremos avanzar hacia el añadiendo un ligero movimiento lateral o rotacional, probablemente se haga evidente el cambio de un frame al siguiente y produciendo un parpadeo.

Hemos de analizar cuidadosamente nuestra escena: ¿hasta qué punto necesito acercarme? ¿quiero moverme muy deprisa o muy despacio? ¿voy a detenerme a observar detenidamente un árbol concreto? Etc. Probablemente para ciertas situaciones se haga necesario emplear una combinación de varias técnicas (billboards tradicionales, nuestros árboles de 2 dimensiones y media, árboles 3d de baja resolución y quizá un sólo árbol 3d con gran detalle y resolución).

Finalmente pensad que está misma técnica se puede emplear para muchas otras cosas que no son árboles: pensad en una sala repleta de cientos de esculturas de terracota prácticamente iguales, o un montón de cadenas que cuelgan verticalmente de una salao.

table border=0 cellpadding=0 cellspacing=0><tbody><tr bgcolor=> <td bgcolor=>desde aquí quiero mostrar mi agradecimiento a mi buen amigo Alberto areta, que me echó una mano con el script (creo que nunca se me hubiera ocurrido usar la orden for next loop de no a ver sido por él). Y también a jens c. Möller, por crear una herramienta tan fabulosa como es xpressionist y por ponerme en la pista de ésta técnica con los árboles 2,5d (a través del propio Alberto).

Cristóbal Vila, diciembre 2006
/td> <td>
/td> </tr> <tr> <td>

</td> <td bgcolor=>
/td> <td>

</td> </tr> </tbody></table> <table border=0 cellpadding=0 cellspacing=0 height=20 width=800> <tbody><tr> <td>
/td> </tr> </tbody></table> nota 1: he intentado ser lo más preciso y exacto posible, pero es probable que exista alguna incorrección en el texto. Si detectas algún error no dudes en hacérmelo saber para proceder a su corrección.

Nota 2: si me quieres ayudar traduciendo los textos de este artículo al inglés, estaré encantado de crear una segunda versión adaptando todos los contenidos a ese idioma, incluyendo una nota de agradecimiento por la traducción y un enlace con tu web y/o email.

.

-- IMÁGENES ADJUNTAS --